Satisfaccion_de_Usuarios--lightGBM
Predicción de la satisfacción del usuario del aeropuerto
Uso de Regresión lightGBM

LightGBM es un framework de potenciación de gradientes que utiliza algoritmos de aprendizaje basados en árboles. Está diseñado para ser distribuido y eficiente, con las siguientes ventajas: 1) Mayor velocidad de entrenamiento y mayor eficiencia; 2) Menor consumo de memoria; 3) Mayor precisión; 4) Compatibilidad con aprendizaje paralelo, distribuido y por GPU; y 5) Capacidad para gestionar datos a gran escala.
Establecer el directorio de trabajo y cargar datos
import os
import pandas as pd
os.chdir('dir')
df = pd.read_csv('airport2809.csv')
df.info()
Importar bibliotecas
import lightgbm as lgb
import numpy as np
import seaborn as sns
from numpy import asarray
from numpy import mean
from numpy import std
from sklearn.datasets import make_regression
from lightgbm import LGBMRegressor
from sklearn.model_selection import cross_val_score
from sklearn.model_selection import RepeatedKFold
from matplotlib import pyplot
Desplegar la matriz de correlaciones
sns.heatmap(df.corr(), cmap='coolwarm')
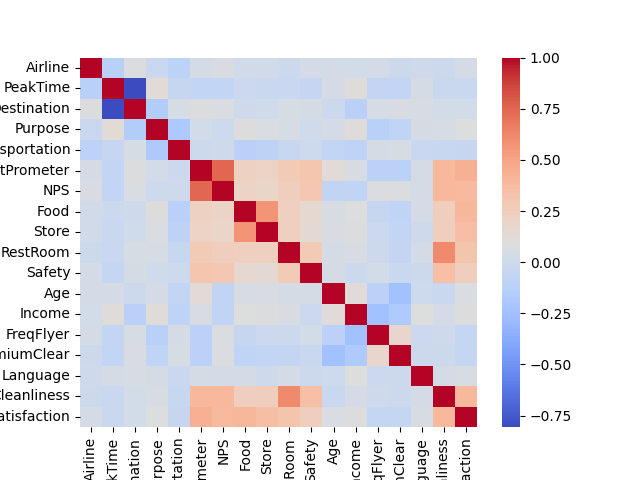
Base de datos: extraer las variables dependiente (target) e independientes (features)
X = df.drop('Satisfaction',axis=1)
y = df['Satisfaction']
Dividir los datos en conjuntos de datos de entrenamiento y prueba
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.30,
shuffle=False,
random_state = 1234)
Inicializar y entrenar el regresor LGBM
model = LGBMRegressor(n_estimators=100, random_state=42)
Ajustar el modelo lightGBM a los datos
model.fit(X_train, y_train)
Hacer predicciones en el conjunto de pruebas
y_pred = model.predict(X_test)
Calcular métricas de evaluación
from sklearn.metrics import root_mean_squared_error
from sklearn.metrics import mean_absolute_percentage_error, mean_squared_error, r2_score, explained_variance_score, mean_absolute_error
mape = mean_absolute_percentage_error(y_test, y_pred)
mse = mean_squared_error(y_test, y_pred)
rmse = root_mean_squared_error(y_test, y_pred)
mae = mean_absolute_error(y_test, y_pred)
r2 = r2_score(y_test, y_pred)
explained_var = explained_variance_score(y_test, y_pred)
Mostrar las métricas de evaluación
print("MAPE, mean absolute percentage error:", mape)
print("MSE, Mean squared error:", mse)
print("RMSE, Root mean squared error:", rmse)
print("MAE, Mean absolute error:", mae)
print("R2, R-squared:", r2)
print("Explained variance:", explained_var)
RESULTADOS
MAPE, mean absolute percentage error : 0.12297041826724223
MSE, Mean squared error 0.46828457144794255
RMSE, Root mean squared error 0.6843132115105937
MAE, Mean absolute error 0.49018020422072434
R2, R-squared 0.3025840635100512
Explained variance 0.30260445796819113
Importancia de las variables predictoras
importance = model.feature_importances_
print(importance)
import matplotlib.pyplot as plt
lgb.plot_importance(model, importance_type='gain', figsize=(10, 6), height=.5, grid=False)
plt.title('Feature Importance (lightGBM)')
plt.show()
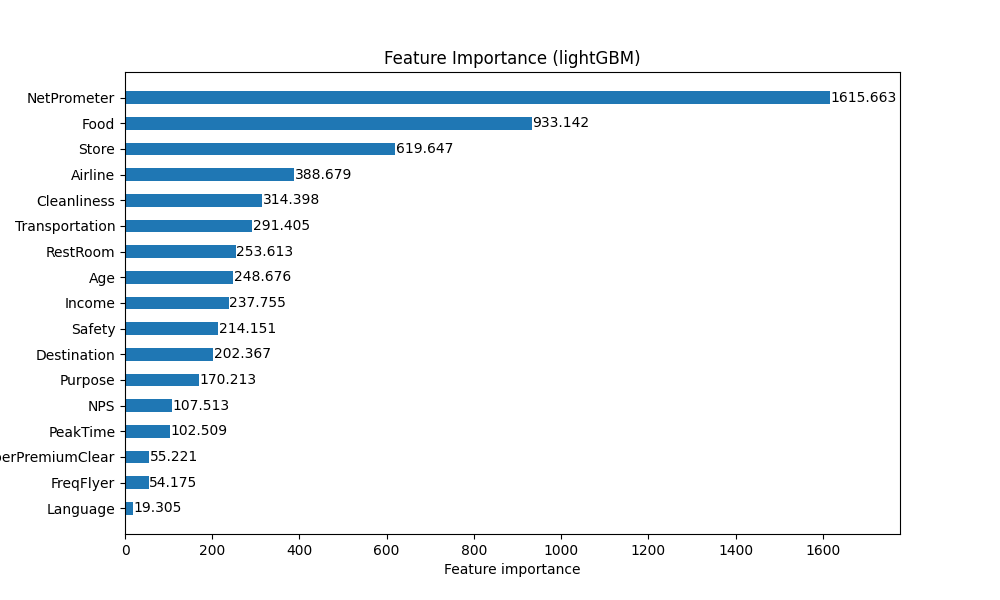
Graficar los valores reales versus los previstos y los residuos reales versus los previstos
import matplotlib.pyplot as plt
from sklearn.metrics import PredictionErrorDisplay
from sklearn.pipeline import make_pipeline
from sklearn.svm import SVR
from sklearn.preprocessing import StandardScaler
rng = np.random.default_rng(42)
X = rng.random(size=(200, 2)) * 10
y = X[:, 0]**2 + 5 * X[:, 1] + 10 + rng.normal(loc=0.0, scale=0.1, size=(200,))
reg = make_pipeline(StandardScaler(), SVR(kernel='linear', C=10))
reg.fit(X, y)
fig, axes = plt.subplots(1, 2, figsize=(8, 4))
PredictionErrorDisplay.from_estimator(reg, X, y, ax=axes[0], kind="actual_vs_predicted")
PredictionErrorDisplay.from_estimator(reg, X, y, ax=axes[1], kind="residual_vs_predicted")
plt.show()
Importancia por Permutación
La importancia de las características por permutación es una técnica eficaz para evaluar la importancia de las características en un modelo de aprendizaje automático. Funciona barajando aleatoriamente los valores de cada característica y midiendo la disminución del rendimiento del modelo. Esto proporciona una estimación más confiable de la importancia de las características en comparación con las medidas de importancia integradas, ya que tiene en cuenta la interacción entre ellas.
from sklearn.inspection import permutation_importance
perm_importance = permutation_importance(model, X_test, y_test, n_repeats=10, random_state=42)
sorted_idx = perm_importance.importances_mean.argsort()
plt.figure(figsize=(10, 6))
plt.barh(range(len(sorted_idx)), perm_importance.importances_mean[sorted_idx], align='center')
plt.yticks(range(len(sorted_idx)), [f'feature_{i}' for i in sorted_idx])
plt.xlabel('Permutation Feature Importance')
plt.ylabel('Feature')
plt.title('Permutation Feature Importance (lightGBM)')
plt.tight_layout()
plt.show()
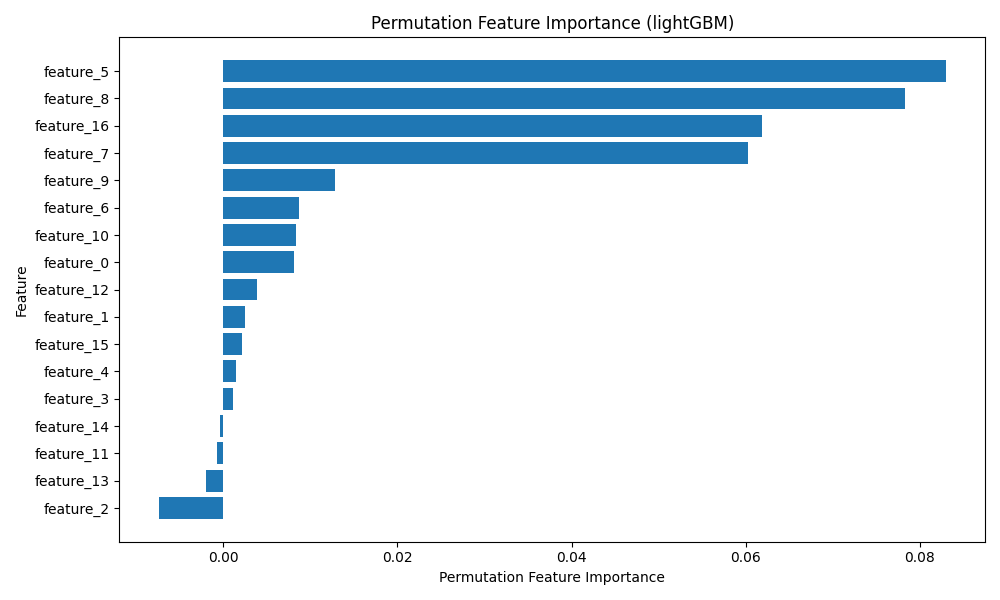
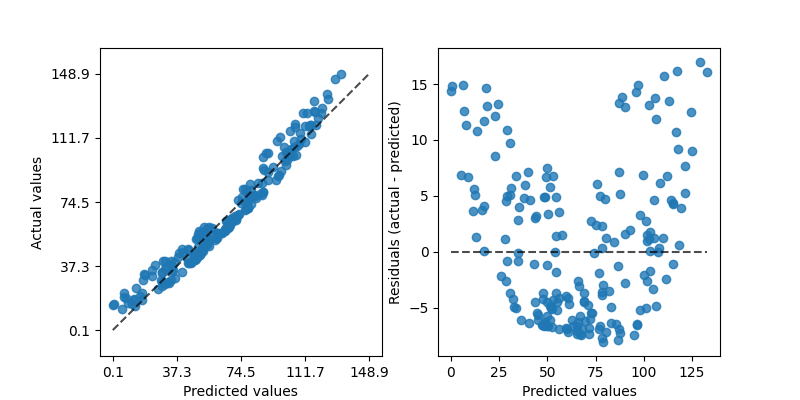
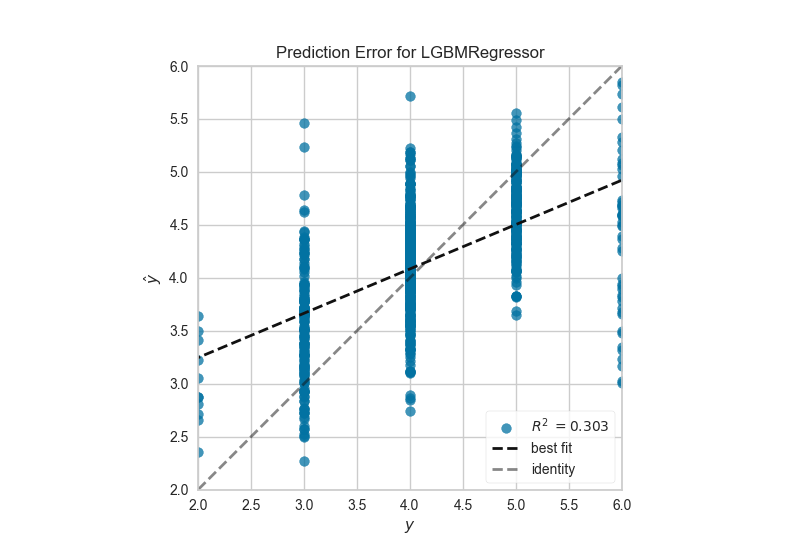
Gráfico del Error de Predicción
Un gráfico de error de predicción muestra los objetivos reales del conjunto de datos frente a los valores predichos generados por el modelo. Esto permite ver la varianza del modelo. Los analistas pueden diagnosticar modelos de regresión utilizando este gráfico comparándolo con la línea de 45 grados, donde la predicción coincide exactamente con el modelo.
import yellowbrick
from yellowbrick.regressor import PredictionError
visualizer = PredictionError(model)
visualizer.fit(X_train, y_train) # Fit the training data to the visualizer
visualizer.score(X_test, y_test) # Evaluate the model on the test data
visualizer.show() # Finalize and render the figure
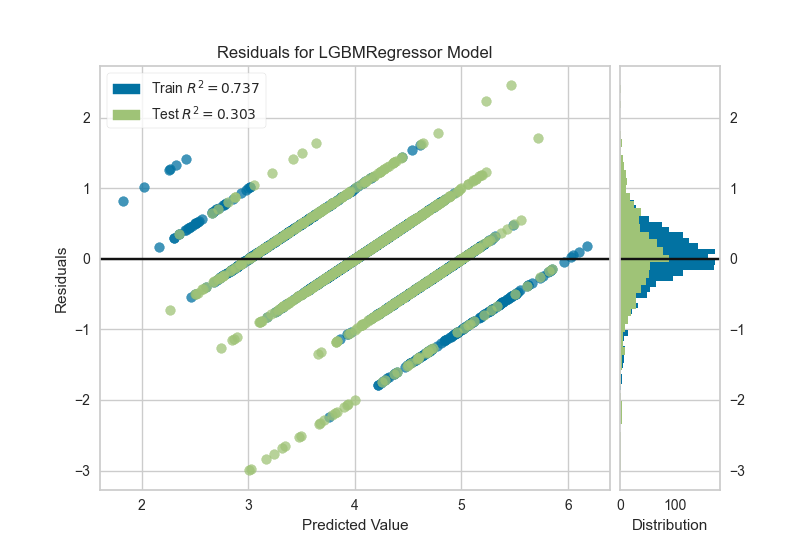
Gráficos de residuos en datos de entrenamiento y prueba
from yellowbrick.regressor import ResidualsPlot
visualizer = ResidualsPlot(model)
visualizer.fit(X_train, y_train) # Fit the training data to the visualizer
visualizer.score(X_test, y_test) # Evaluate the model on the test data
visualizer.show() # Finalize and render the figure