Satisfaccion_de_Usuarios--Machine_Learning

Predicción de la Satisfacción de Usuarios de un Sitio Web mediante Machine Learning

Regresión de aprendizaje automático de XGBoost optimizada con Optuna

El algoritmo XGBoost significa “Impulso de Gradiente Extremo”. Se centra en la velocidad computacional y el rendimiento del modelo. Optuna es un marco avanzado de optimización de hiperparámetros con visualizaciones para mayor interpretabilidad.

Código Python:

1. Establecer el directorio de trabajo y cargar los datos

import os
os.chdir('C:/Users/Alejandro/Documents/')
import pandas as pd
data = pd.read_csv('website365.csv')
data.info()

2. Importar bibliotecas

import numpy as np
import pandas as pd
import xgboost as xgb
import optuna
from sklearn.datasets import make_regression
from sklearn.model_selection import train_test_split
import matplotlib.pyplot as plt
import seaborn as sns

3. Separar las variables target y features

X = data.drop('Satisfaction', axis=1)
y = data['Satisfaction']

4. Dividir los datos en conjuntos de entrenamiento y prueba

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

5. Usar Optuna para optimizar los hiperparámetros del modelo XGBoost

Definir la función objetivo para Optuna.

from sklearn.metrics import root_mean_squared_error

def objective(trial):
    params = {
        'objective': 'reg:squarederror',
        'eval_metric': 'rmse',
        'booster': trial.suggest_categorical('booster', ['gbtree', 'gblinear', 'dart']),
        'lambda': trial.suggest_float('lambda', 1e-8, 1.0, log=True),
        'alpha': trial.suggest_float('alpha', 1e-8, 1.0, log=True),
        'max_depth': trial.suggest_int('max_depth', 1, 9),
        'eta': trial.suggest_float('eta', 1e-8, 1.0, log=True),
        'gamma': trial.suggest_float('gamma', 1e-8, 1.0, log=True),
        'grow_policy': trial.suggest_categorical('grow_policy', ['depthwise', 'lossguide']),
        'n_estimators': trial.suggest_int('n_estimators', 50, 500),
        'subsample': trial.suggest_float('subsample', 0.1, 1.0),
        'colsample_bytree': trial.suggest_float('colsample_bytree', 0.1, 1.0),
        'min_child_weight': trial.suggest_int('min_child_weight', 1, 10),
    }
    
    model = xgb.XGBRegressor(**params, random_state=42)
    model.fit(X_train, y_train, eval_set=[(X_test, y_test)], verbose=False)
    preds = model.predict(X_test)
    rmse = root_mean_squared_error(y_test, preds)
    return rmse

6. Llevar a cabo la optimización Optuna

study = optuna.create_study(direction='minimize')
study.optimize(objective, n_trials=50, show_progress_bar=True)

7. Entrenar el modelo final con los mejores hiperparámetros

best_params = study.best_params
best_params['objective'] = 'reg:squarederror'
best_params['random_state'] = 42

final_model = xgb.XGBRegressor(**best_params)
final_model.fit(X_train, y_train, eval_set=[(X_test, y_test)], verbose=True)

8. Evaluar el modelo

y_pred = final_model.predict(X_test)

print("\nEvaluation Metrics:")

Calcular las métricas de la evaluación

from sklearn.metrics import mean_absolute_percentage_error, mean_squared_error, r2_score, explained_variance_score, mean_absolute_error

mape = mean_absolute_percentage_error(y_test, y_pred)
mse = mean_squared_error(y_test, y_pred)
rmse = root_mean_squared_error(y_test, y_pred)
mae = mean_absolute_error(y_test, y_pred)
r2 = r2_score(y_test, y_pred)
explained_var = explained_variance_score(y_test, y_pred)

Desplegar las métricas de evaluación

print(f"MAPE, mean absolute percentage error:", round(mape,5))
print(f"MSE, Mean squared error:", round(mse,5))
print(f"RMSE, Root mean squared error:", round(rmse,5))
print(f"MAE, Mean absolute error:", round(mae,5))
print(f"R2, R-squared:", round(r2,5))
print(f"Explained variance:", round(explained_var,5))

RESULTADO

Evaluation Metrics:

MAPE, mean absolute percentage error: 0.01529

MSE, Mean squared error: 0.02494

RMSE, Root mean squared error: 0.15792

MAE, Mean absolute error: 0.06406

R2, R-squared: 0.99271

Explained variance: 0.99331

9. Gráficos

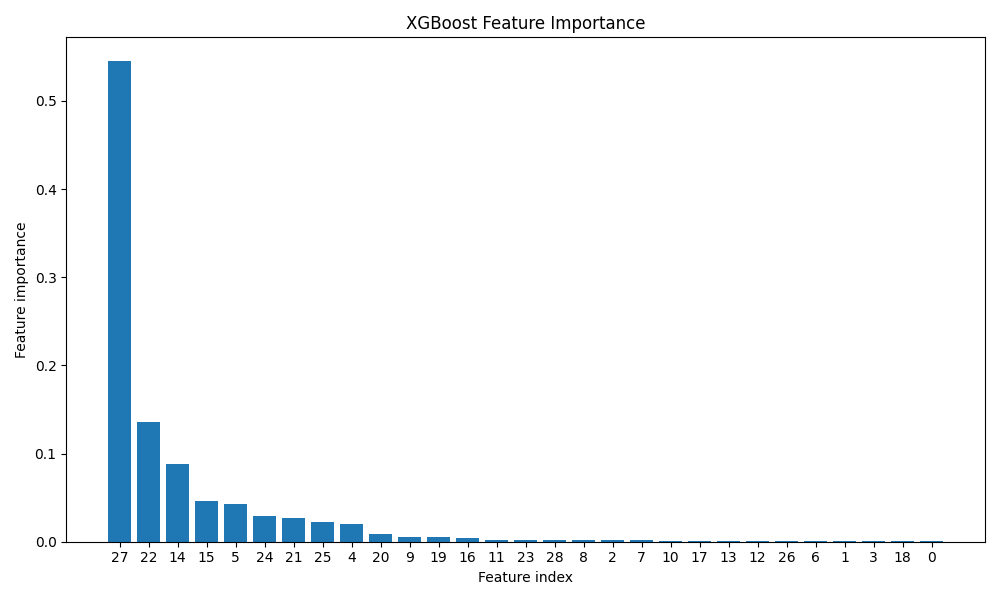
Gráfico de importancia de las variables predictivas

feature_importance = final_model.feature_importances_
sorted_idx = np.argsort(feature_importance)[::-1]

plt.figure(figsize=(10, 6))
plt.bar(range(X.shape[1]), feature_importance[sorted_idx], align='center')
plt.xticks(range(X.shape[1]), sorted_idx)
plt.xlabel('Feature index')
plt.ylabel('Feature importance')
plt.title('XGBoost Feature Importance')
plt.tight_layout()
plt.show()

Graficar valores reales y predichos

plt.figure(figsize=(8, 8))
sns.scatterplot(x=y_test, y=y_pred, alpha=0.6)
plt.plot([min(y_test), max(y_test)], [min(y_test), max(y_test)], '--r')
plt.xlabel('Actual Values')
plt.ylabel('Predicted Values')
plt.title('Actual vs Predicted Values')
plt.show()

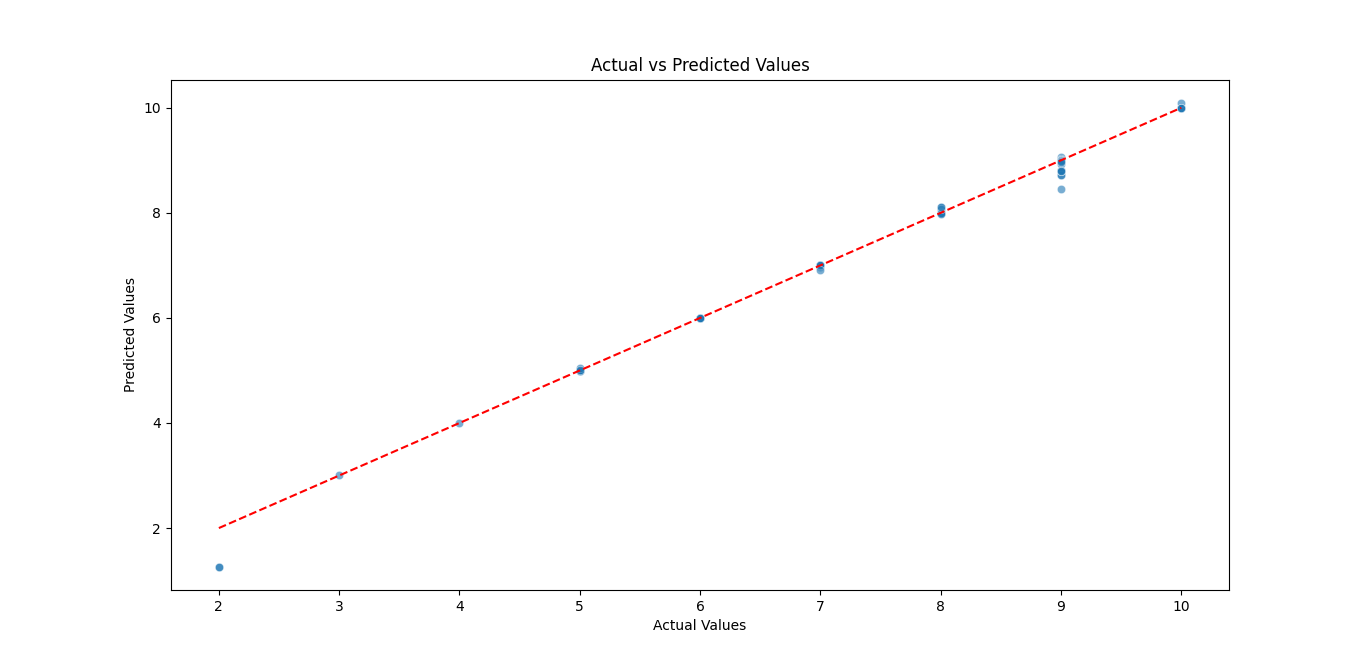
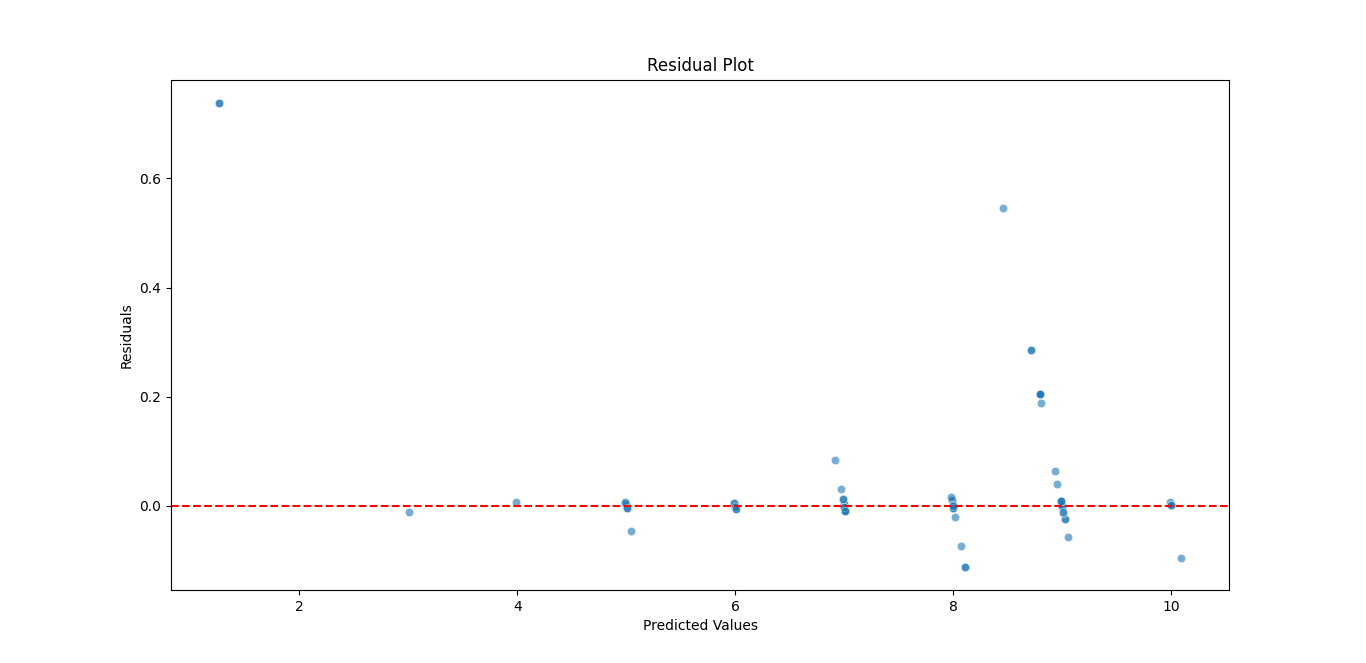
Grafico de los residuos

residuals = y_test - y_pred
plt.figure(figsize=(8, 6))
sns.scatterplot(x=y_pred, y=residuals, alpha=0.6)
plt.axhline(y=0, color='r', linestyle='--')
plt.xlabel('Predicted Values')
plt.ylabel('Residuals')
plt.title('Residual Plot')
plt.show()

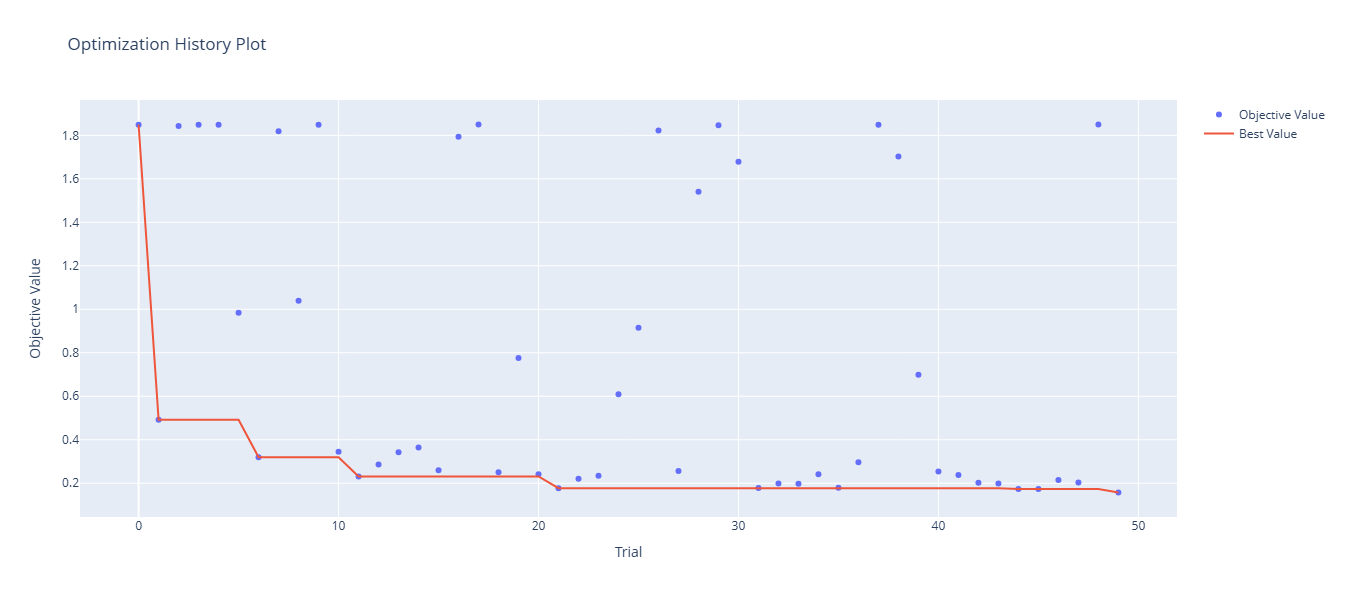
Graficar el historial de optimización

optuna.visualization.plot_optimization_history(study).show()

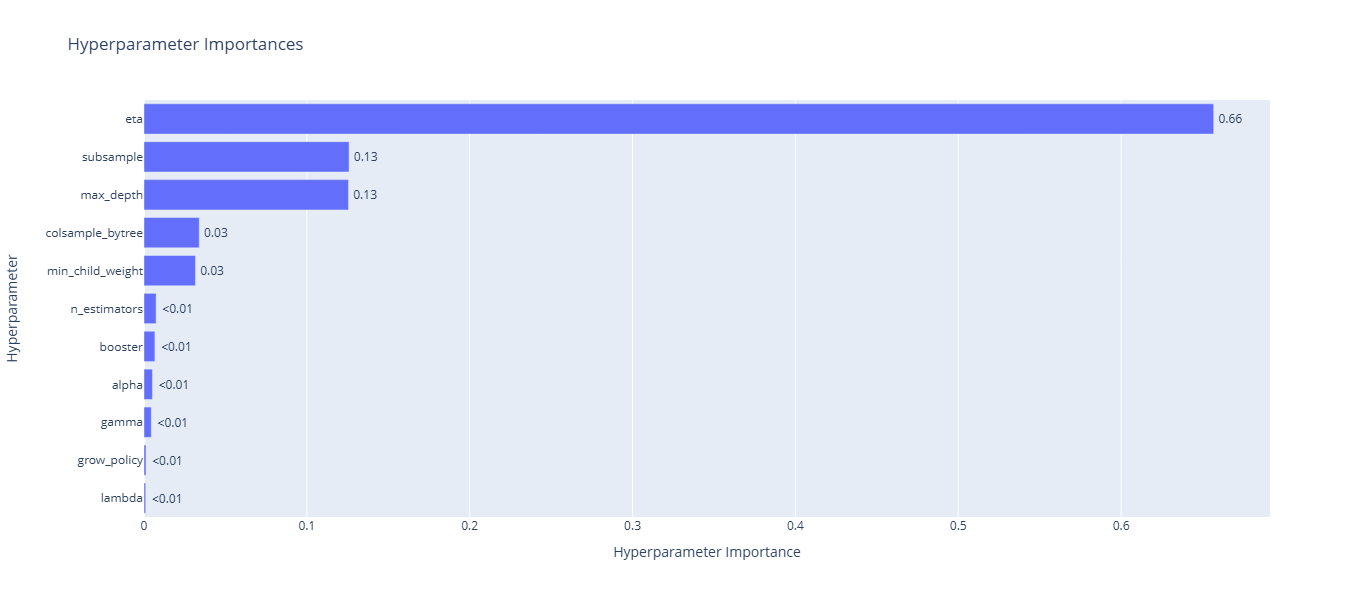
Graficar la importancia de los parámetros

optuna.visualization.plot_param_importances(study).show()